登录航海网,拥抱全世界
您需要 登录 才可以下载或查看,没有账号?立即注册
x
本帖最后由 小虫宁宁 于 2022-3-10 10:25 编辑
海图数学基础
1 什么叫海图投影?
海图上为什么用海图投影?这是一个常令初学者迷惑的问题。我们知道,地球表面用数学语言来措述则是一个不可展的曲面,而海图是一个平面。不可展曲而能否拉成平而?
我们从日常生活中不难得出结论,假若将橘子皮或西瓜皮硬要压成平面,就必然会产生不规则的裂口和福皱。同理,不可展曲面与平面的关系也是如此。我们知道海图必须是连续的、平整的平面,不允许有重叠和裂口的现象存在。这如何来解决不可展的曲面与平面之间的矛盾?就必须用数学方法即投影的方法来解决用投影方法来解决这一矛盾,人们经过了长期的探索和研究。最初用儿何透视方法。
假如地球是一个透明体,在地球中心放置一个光源,将地球面上经线和纬线投影到平面、圆柱面、圆维面等投影面上。将圆柱面或圆锥面沿某一条母线切开,就可得到圆柱或圆锥投影。
后来出现了数学分析这门学科,投影中就开始应用数学分析方法,因而几何透视法就很少用了。目前投影的研究方法主要是数学分析方法。但从系统性和全面性的角度来说,投影有透视、非透视之分(数学分析法为非透视)。
用透视或非透视方法建立海图投影,虽然解决了球面与平面之间的矛盾,但做到百分之百的准确无误是不可能的,必定会产生一些变形(如长度、面积、角度变形),因此研究海图投影除了研究建立投影的方法之外,还必须研究海图投影的变形,并且可以通过一定的方法使某种变形不存在,或减少一些变形,或使变形分布均匀一些,以满足不同海图品种的需要。
海图变形一般用变形椭圆、变形表、等变形线和坐标曲线表示。
那什么叫海图投影呢?简单地讲,海图投影是运用一定的数学法则将地球表面的经纬线相应的投影到平面上的理论和方法。其方法是把地球椭球面上各点的地理坐标转换为平面上相应的平面直角坐标,建立海图的经纬网,构成海图的“骨架”。
2 海图上常用哪几种投影?
我国海图常用的投影有墨卡托投影、高斯一克吕格投影、日晷投影、平面图投影四种。
(1)墨卡托投影的概念与特性是什么?
1.墨卡托投影的概念墨卡托投影又叫等角正圆柱投影。由著名制图学家墨卡托所创制,并于1569年首先用于编制海图,故称为墨卡托投影。墨卡托投影非常适合于编制航海图,因此,四百多年来,世界上各国的航海图一般都采用墨卡托投影。
2.墨卡托投影的坐标表达式及变形公式
根据经纬线长度比相等的条件,推导出墨卡托投影

3 墨卡托投影的特性墨卡托投影主要有三个特性第一,经纬线格网为矩形,计算简单,绘制方便。
由投影坐标公式,可知,墨卡托投影的经线等间隔:纬线不等间隔,纬度越高间距越大,我们称这种现象为渐长性。
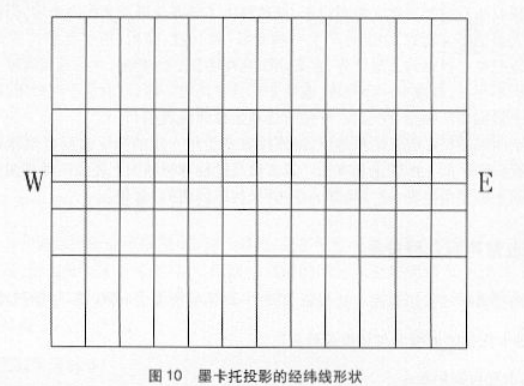
第二,墨卡托投影为等角投影,能保持实地方位与图上方位的一致性,在图上作业十分方便,无需进行角度改正。
第三,在墨卡托投影中,等角航线投影成直线,非常有利于海图作业。
由于墨卡托投影具有上述三大特性,使其成为航海图的首选投影。
4 墨卡托投影的变形规律由于墨卡托投影是等角性质的投影,故只存在着长度变形和面积变形。
其变形情况可根据变形公式来进行精确计算和分析。
设基准纬度为±30°,纬差每隔15°,算出的各种变形数值见表10-1:
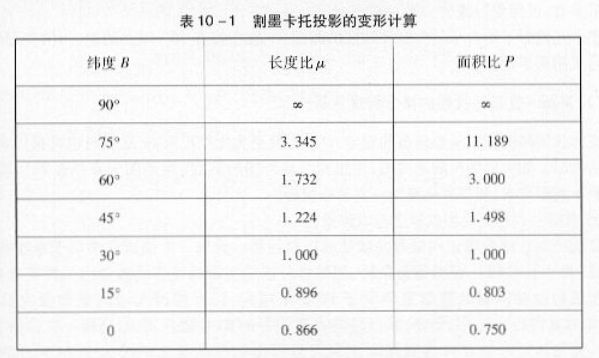
由表中可以看出,割墨卡托投影的变形规律为:
在两条基准纬线±B。上长度比为1,无变形:
在两条基准纬线(一B。,B。)之间,所有的纬线圈半径大于椭圆半径,投影后缩小,长度比小于1,为负向变形:
在两条基准纬线之外(-B。,-90°)和(B。,90°),纬线圈半径小于椭圆半径,投影后放大,长度比大于1,为正向变形:
两极处(±90°)长度比为无穷大:
面积比是长度比的平方,面积变形很大,产生失真现象,如格陵兰岛的实际面积仅为南美洲的八分之一左右,但在墨卡托投影海图上,格陵兰岛的面积比南美洲的面积还大。
对于切墨卡托投影,根据切墨卡托投影的长度比公式,也可以计算出其变形情况。自赤道向两极每隔10°计算,所得长度比数值见表10-2:
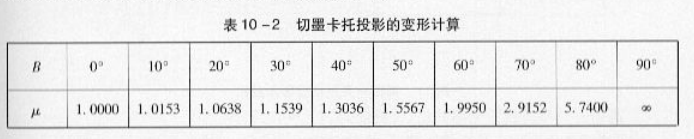
从上表可以得到切墨卡托投影的变形规律:
赤道没有变形;
纬度越高,变形越大;
至地球极点处,变形为无穷大。
根据墨卡托投影的变形规律,可以得出如下结论:
切投影用于制作沿赤道延伸地区的海图,而割投影用于制作沿纬线延伸的地区的海图。
我国海域位于北半球,因此,我国海域的海图一殷都采用割墨卡托投影。因此,选好基准纬线非常重要,可使变形减少一半左右。
墨卡托投影不适合于制作高纬地区的海图,一殷在纬度75”以上的地区,因变形较大,不宜再采用墨卡托投影。
(2)高斯一克吕格投影的概念和规定是什么?
按照我国海图制图编绘规范的规定,1:2万及更大比例尺海图,必要时也可采用高斯一克昌格投影。如大比例尺的港湾图,考虑到与地形图的衔接(地形图为高斯投影),或投影变形遁于制图要求,便要采用高斯一克吕格投影。
1 高斯一克吕格投影的概念与投影条件高斯一克吕格投影也叫做等角横切椭圆柱投影。设想一个椭圆柱横切于地球椭球某一经线(即中央经线),根据等角条件,用数学分析方法得到经纬线映象的一种等角投影。
该投影最初由德国著名数学家高斯于1822年拟定,后经德国大地测量学家克昌格在1912年对其进行了补充、完善,从面使其具有很好的实用价值,故名高斯一克吕格投影。
高斯一克吕格投影是我国编制基本比例尺地形图的投影和比例尺大于1:2万的海图投影。
其投影条件为:
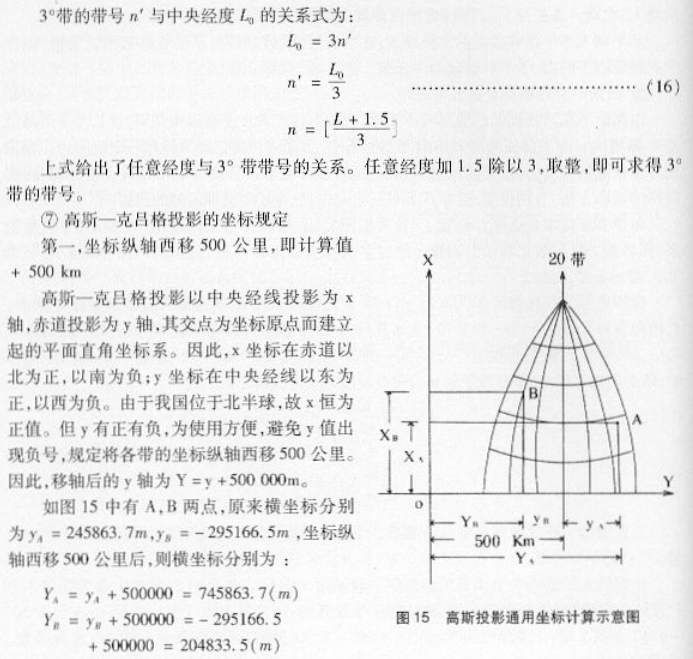
中央经线和赤道投影为平面直角坐标系的坐标轴,且投影经纬线以两轴为对称:投影后无角度变形:中央经线投影后保持长度不变。见图11。
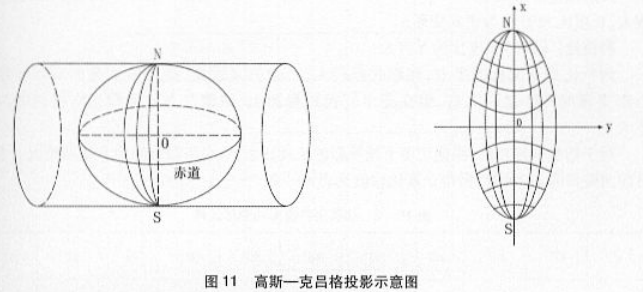
2 高斯一克吕格投影坐标的正、反解公式根据投影条件可推出高斯投影的正,反解公式。
由地球表面的经纬度求解海图平面直角坐标的投影计算叫做正解。高斯一克吕格投影坐标的正解公式为:

由海图平面直角坐标反求地球表面的经纬度的投影计算叫做反解。高斯一克吕格投影坐标的反解公式为:
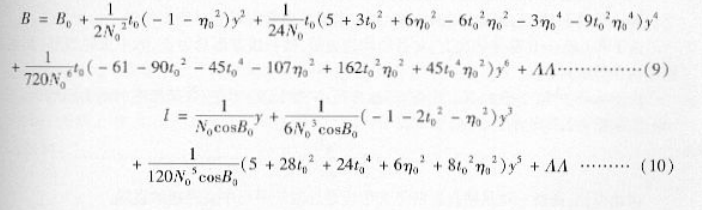
B,L以弧度为单位,若换为度,则乘p°,即

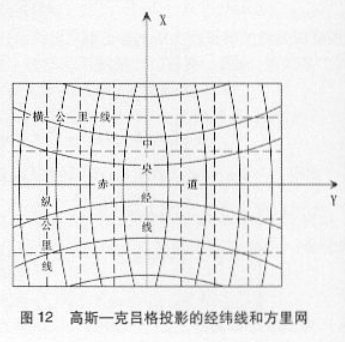
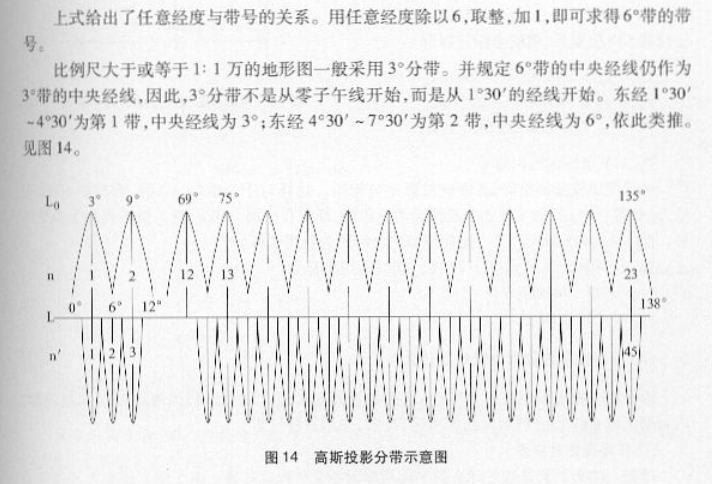
③高斯一克吕格投影的经纬线和方里网形状
中央经线和赤道投影后成相互垂直的直线,分别与是卡托投影图上的经线和赤道重合:其余经线为凹向中央经线的曲线,并对称于中央经线:其余纬线为凸向赤道的曲线,并以赤道为对称轴。因为经纬线为曲线,量测起来不方便,因此,在高斯一克吕格投影海图上展绘平行于中央经线和泰道的两组直线,构成方里网。参见图12。
④高斯一克吕格投影的长度比等角投影中任意一点长度比与方向无关,根据这一条件,可以推出高斯一克吕格投影的长度比公式:
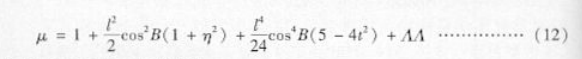

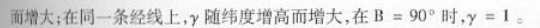


(3)日晷投影的概念与特性是什么?
由于墨卡托投影在纬度75以上地区的投影变形很大,因此,我国海图编绘规范规定当制图区域60%以上的地区纬度高于75时,采用日晷投影。
①日晷投影的概念
球面上的大圆弧是通过球心的平面与球面相交所截成的弧。由于球上任意大圆都含有球心,如以球心为视点,则其视线与任一大圆所构成的视平面都是大圆平面。扩展大圆平面与投影平面相交,这两平面的交线必定是直线。这条直线就是大圆弧在平面上的投影。参见图16。
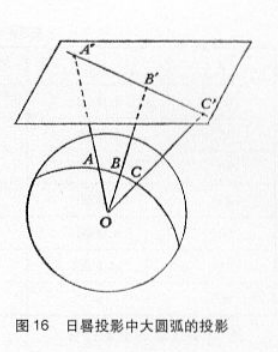
用这种方法所得的投影,叫做球心透视方位没影或叫心射投影。因为这种投影好像利用日影测定时问的一种仪器的原理一样,故又称为日晷投影。
②日晷投影的基本公式
割日晷投影公式为:

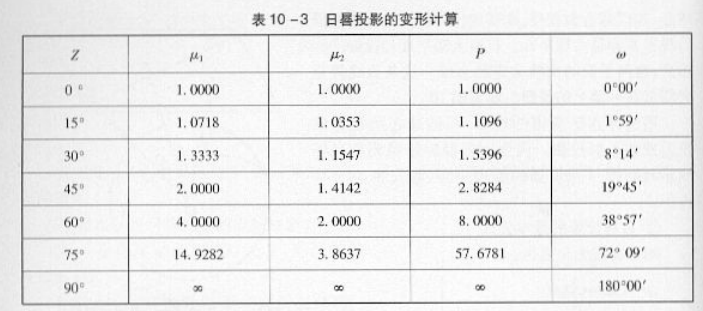
3 日晷投影的变形规律根据日晷投影变形公式,可计算其各种变形,计算结果见表10一3:
从变形表来看,球心投影变形较大,只有在投影中心点变形较小,而在其他处变形则是很大的,尤其是其角度变形大。它属于任意投影的一种。
4 日晷投影的重要特性
球心投影具有大圆投影成直线的重要特性,即地球面上任何大圆弧经球心投影后,在平面上的表象均为直线,这一特性在航海上非常有价值。
虽然墨卡托投影解决了等角航线为直线的问题,给了船舶在海上活动的便利。但是,等角航线并不是实地两点间的最短距离。在球面上,两点间的最短距离是大圆死,称为大圆航线。沿着等角航线航行航程远,这点在近海航行时还不显著,但在远洋航行时矛盾就比较突出了。如由非洲南端的好望角到澳大利亚南端的墨尔本,若沿大圆航线走,航程为5450海里,若按等角航线走,则航程为6020海里,要多走576海里(约1050千米)的路程。因此,船舶在作远洋航行时,最好能沿着大圆航线航行。这就要求在海图上能比较简便地确定出大圆航线的位置,并且大圆航线在海图上都投影为直线,在海图上任意两点之间所连的直线就是大圆航线。由于在日晷投影中大圆航线投影成直线,因此,远洋航行图一般采用日晷投影。航海时若沿此方向航行则距离最短。但是由于日晷投影变形较大,也不等角,因此,一般不直接用日晷投影海图来进行航行。为兼顾到走捷径和便利航海作业,有经验的航海家远洋航行时,通常先把日晷投影图上所确定的大圆航线的位置转绘到墨卡托投影海图上的相应位置上,然后按墨卡托投影海图上标绘的大圆航线再作等角航行。
5 日晷投影的经纬线形状
以切投影为例,日晷投影的投影公式为:

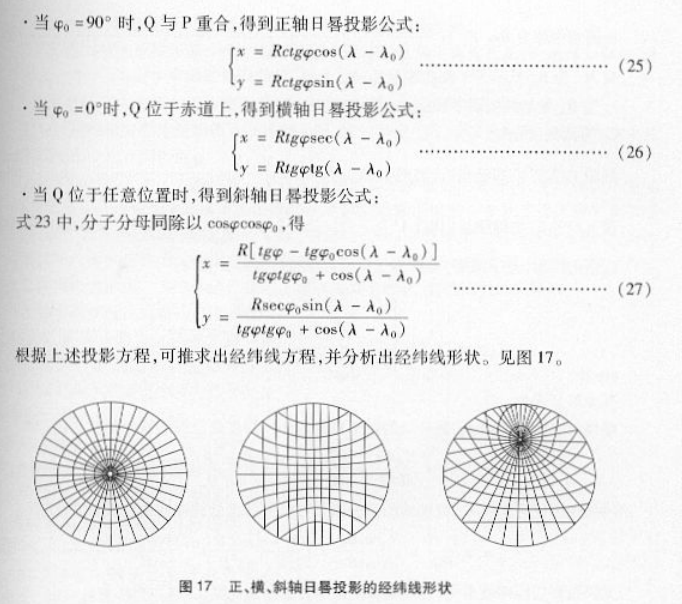
(4)平面图投影是怎样定义的?
平面图用于大比例尺海图的投影,我国大比例尺(大于1:2万)海图除可采用高斯一克吕格投影外,也曾经采用过平面图投影。因此,了解平面图投影对于认识和使用过去的海图资料也有一定的帮助。
①平面图投影概念平面图投影就是把地球面上的小块面积看做是平面,把经纬线看成是平行而各自间隔相等的直线,经纬线互相垂直,它属于正轴圆柱投影。
②平面图投影条件平面图投影主要具备三个条件:
第一,取本图中纬处经差1分的纬线的实地弧长(纬线1'长)作为任一纬线经差1分的投影长:
第二,取本图中纬处纬差1分的经线弧的实地弧长(经线1'长)作为任一经线纬差1分的投影长;第三,经纬线投影为两组互相平行的直线。
③平面图投影公式


3 地球形状是怎样描述的?
(1)地球的几何形状是怎样描述的?
受科学技术发展程度的限制,自古至今人们对地球形状和大小的认识由肤浅至深入,由概路到精确,由不正确到正确。归纳如下,历史上人们对地球的认识大约有以下几种。
“天圆地方”学说:远古人们认为地球是一个广袤无边的平面。
“浑天说”:认为地球不是一个平面而是一个圆球。认为宇宙好比鸡卵,地球为卵黄,悬浮于宇宙之中。
“地球自转”:古希腊学者赛里斯等提出地球绕地轴自转。
葡萄牙航海家麦哲伦组织船队绕地球一周,进一步证实了地球为球形。地球为球形是地球形状的第一次几何近似。
公元17世纪,开始了大地测量。通过对地球的实际测量的计算分析,发现地球不是球体,其表面是一个接近于大地水准面的形状。所谓大地水准面是一个处于流体静平衡状态的海洋表面(无波浪、水流、潮汐和大气变化引起的扰动)并延伸到大陆内部的水准面,海洋上通常以平均海水面作为大地水准面的基础面,它是一个连续封闭曲面。大地水准面所包围的形体叫做大地体。大地体已经接近了地球的真实形状,它是高程的起算面。
大地水准面远比地球的自然表面规则了许多,但到目前为止还找不到一种数学公式把它表现出来。这是为什么呢?因为大地水准面上的重力位势是处处相等的,并在该面上任何一点的铅垂线都与大地水准面正交。而铅垂线(重力方向)的方向受地球内部分布不均匀的影响,致使大地水准面产生微小的起伏,因而该面是不规则的几何曲面。
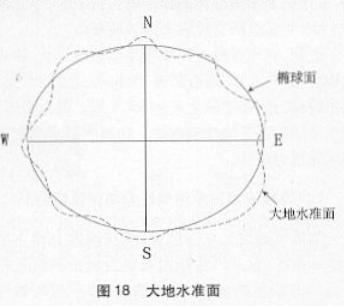
物理学家牛顿认为地球赤道离心力最大,两极最小,要保持平衡,地球一定是扁平状态。大地测量学家通过实践证实地球表面接近于具有微小扁率的旋转椭球面,即以椭圆的短轴(地轴)为旋转的椭球面。用这种椭球面来代替地球的形状称之为地这是一个纯粹的数学表面,用数学公式可以表示,在其上运算也简单方便。这是地球表而的第二次几何近似。

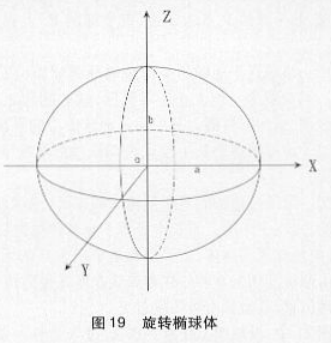

在上述5个基本元素中,a、b为长度值,a,e,e'均表示地球椭球的扁平程度。要决定地球椭球体的形状和大小只要知道五个基本元素中的两个就可以了,但其中至少有一个长度元素a或b。
不同国家在不同时期往往采用不同大小的地球椭球体。每个国家必须选择一个与本国领土密合最好的地球椭球体,称为参考椭球体。我国1952年曾采用海福特椭球体制作地形图,采用白塞尔椭球体制作海图。自1953年起地形图开始采用克拉索夫斯基椭球体。海图于1955年也改用克拉索夫斯基椭球体。
近来,利用卫星大地测量测定地球形状,测得大地水准面是一个近似梨形的形状。它在北极突出18.9米,南极凹进25.8米,北纬45地区凹陷5米,南纬45°地区隆起5米,地球赤道为椭圆,长、短半径之差为69.5米。因为梨形地球表面也无法用确切的数学公式表示,故现在常用的还是地球椭球面。当海图要求精度不高或制作小比例尺海图时,为计算方便,常把地球视为球体。
(2)地球表面的地理坐标是如何规定的?
为确定地面上点的位置,须在地面上建立地理坐标系统,它是以地球南北极为极由两组互相垂直的曲线所构成,一组叫做经线,一组叫做纬线。参见图20。
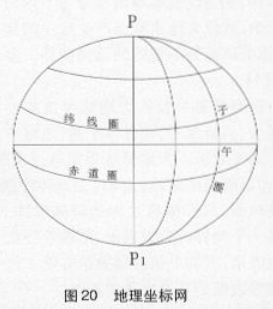
设PP,为地球的自转轴,简称地轴。地轴与地球椭球面(或球面)的两个交点P、P叫做地理坐标极,北半球的P点叫北极,南半球的P,点叫南极。
用一组垂直于地轴的平面截地球椭球面(或球面),其交线为一组大小不等的圆,这些圆称之为纬线圈,或叫平行圈。其中通过地球中心的平面截得的最大的纬线叫做赤道。赤道的圆半径等于地球椭球的长半径a,向两极纬线圈的半径越来越短,在两极点处为两个半径为零的点圆。
用一组通过地轴的平面截地球椭球面(或球面),其交线为一组大小不等的椭圆称之为经线圈,或叫子午圈。其长半径等于地球描球的长半径,其短半径等于地球椭球的短半径b。若将地球视为球体,则经线圈是半径为R的大圆。
由两组互相垂直的经线和纬线在地球表面构成地理坐标网,即可确定地面上任意一点的地理位置,其坐标由经纬度定义。
图21中,设地面上任意一点A,过A点作一条垂线,使该垂线垂直于A点的切平面,此平面称为椭球面上A点的法线,法线与赤道面的夹角B,叫做A点的地理纬度,也称大地纬度(lude)。在同一纬线上各点的纬度B是相等的,不同纬线上点的纬度值不相同。在赤道上纬度为0°,从赤道向两极纬度值增加,极点纬度值为90°。为区别赤道以南,以北,特规定:赤道以北的纬度叫做北纬,注记采用字母W表示:赤道以南的纬度叫做南纬,注记采用字母S表示。
为便于计算,规定北纬用''+”表示,规定南纬用“一”表示.

地球椭球面上的地理坐标建立之后,就建立了地面点与地理坐标一一对应的关系,即地球椭球面上任意一点都有完全确定的纬度和经度;反之如果已知某点的纬度B和经度L,在地球椭球面上完全可以找到这个点。
(3)首子午线有哪些用处?
地球表面通过两极的子午线(经线)很多,为了确定球面上物体的位置,必须确定一条子午线作为初始子午线。地理学家和制图学家把通过英国伦敦格林尼治天文台的经线叫做起始子午线,又叫本初子午线,零子午线或首子午线等。格林尼治天文台位于伦敦郊区。为什么当初要选择通过格林尼治天文台的经线作为首子午线呢?可能是因为公元19世纪以前的英国是世界上最发达的资本主义国家,航海业发达,海图以格林尼治天文台(当时较有名)作为经线的起点制作,而且编制了很多世界海洋中的海图,后来其他各国就以格林尼治天文台作为子午线的基准。目前,格林尼治天文台早就不再用于观测天文,仅作为测算点和东西经度的分界线。在天文台的前面,有一长10米的直线,由南极、北极通过该点的直线就叫做首子午线。同时,这也是时区起始线,全球经度每隔15°为一个时区。天文台门口挂有一口钟,专门为全世界指示时间。地球东西半球的分界也与格林尼治天文台有着密切的联系。习惯上,把通过首子午线以西20°和首子午线以东160°的经线圈作为东西半球的分界线,即从西经20°向东到东经160°为东半球,而从西经20°向西到东经160°则为西半球。因为格林尼治天文台有那么多的作用,英国早已将其作为旅游景点开放,每天都吸引着世界各地的游客来此观光旅游。
4 什么叫基准纬度?
地图投影中不变形的纬线称之为标准纬线,往往指投影面与地球表面相切或相割的纬线。标准纬线对应的纬度叫做标准纬度。海图上习惯把标准纬线和标准纬度分别叫做基准纬线和基准纬度。见图22。
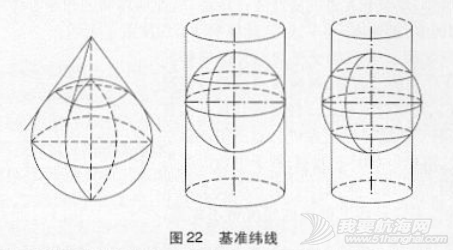
墨卡托投影中确定基准纬线非常重要,因为选好了基准纬线,可以大大减小投影变形。
墨卡托投影中确定基准纬线的方法主要有两种:
(1)理论上如何选取?
为减小投影变形,且使投影变形均匀,选择基准纬线时,一般按照制图区域内最大正向变形与最大负向变形绝对值相等的条件来选取基准纬线。
(2)实际是怎样规定的
一般根据多年海图制图经验,由海图制图部门直接作出规定。目前,民用航海图的基准纬线规定为:
同比例尺的成套航行图以制图区域中纬为基准纬线:其余图以本图中纬为基准纬线,基准纬线取至整分或整度。
对于军用航海图,其基准纬线规定有特殊规定。如墨卡托投影所取的基准纬线一般应取本图中纬(取至整分或整度):成套图,为了便于相邻图幅的拼接,应按照不同海区,采用分区统一标准。
5 什么叫渐长区间、渐长纬度、制图单位?
航海人员在使用墨卡托投影海图资料时,经常会看到渐长区间、渐长纬度、制图单位等概念,而且也很容易把它们弄混滑,为此,有必要专门介绍之。
(1)渐长区间是如何定义和计算的?
由于墨卡托投影的纬度具有渐长性,因而也就有一个在多大范围内可以用等分代替计算的距离问题,我们把以等分代替计算的这个纬度范围称为纬度渐长区间,简称渐长区间。在渐长区间内可以进行等分作业,而不需要进行计算。海图上的经纬线格网不是随意展绘的,如果展绘过多,虽然精度高了,用起来也方便,但会影响到海图的清晰度和对其他要素的表示:如果经纬线格网间隔过大,海图清晰度提高了,但精度不够,不能进行等分作业。所以,在大比例尺海图上展绘经线和纬线的条数也是根据渐长区间来确定的,通常经纬网间隔都小于渐长区间。因此,在每个经纬线格网中都可以进行等分操作。但在小比例尺海图上,由于不进行等分海图作业,因此经纬线间隔可大于渐长区间。
渐长区间计算公式如下:
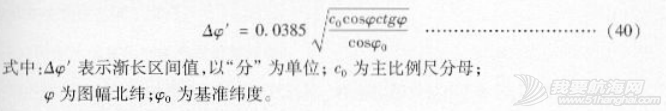
(2)渐长纬度是如何定义与计算的?
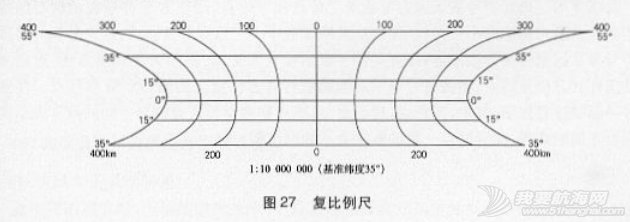
以分为单位的等量纬度叫做渐长纬度,用字母D'表示,其计算公式为:
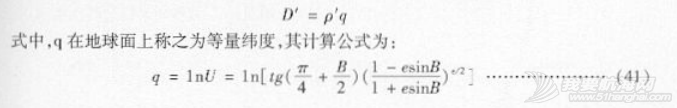
(3)制图单位是如何定义与计算的?
海图上基准纬度线上1'的长度叫做制图单位或图的单位,用字母e。表示,其计算公式为:
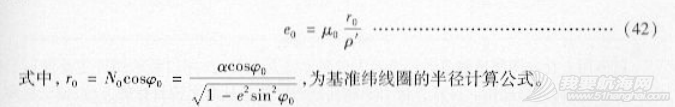
由于墨卡托投影海图的纬线投影长度都是等长的,所以。也是图上纬线一分的长度。知道制图单位的概念很重要,用经差与制图单位相乘,就可以算出任意经度处纬线的长度。
根据制图单位和渐长纬度,可写出墨卡托投影的实用计算公式:
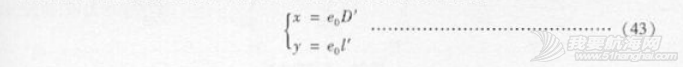
6 海图怎样定向?
海图是具有方位的。海图方位就是解决海图的定向问题。习惯上,人们将海图的定向为:上北、下南、左西、右东。对于航海图,主要用于航海和军事,对海图的方位要求精确,规定经线指示南北,纬线指示东西。为便于航海人员在图上标绘方位,每幅海图上一般配置1~2个罗经圈,又叫方位圈。方位圆采用圆周角法0-360细分,以五角星指示的方向表示罗经图真北方向,也就是经线方向(0),箭头方向为磁北方向,两者的夹角称为磁偏角。方位圈上还表示磁差和年差,磁差和年差用代数和进行运算,两者相同时用“+”表示,两者相反时则用“一”表示。水平中心线的左侧标注磁差和推算年份,右侧标注年差,其中,磁差注记到整分,年差注记至分以下一位小数。见图23。
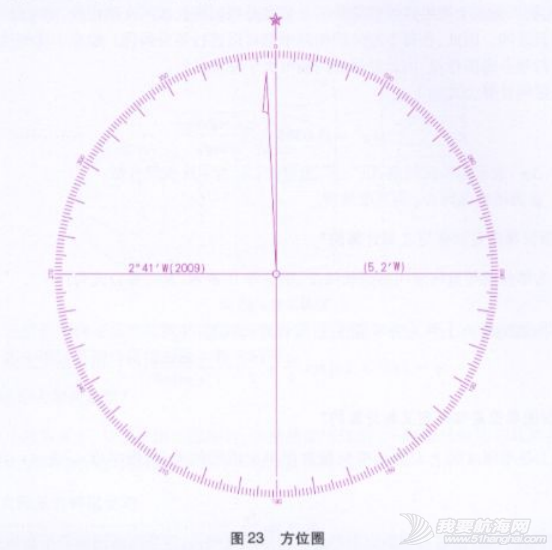
航海图上在内图廓里侧有时还绘有方位引示线及其注记,用以量绘图外主要航行目标的方位,供航海人员使用。注意方位引示线注出的度数是从海上视目标的方位,便于航海人员从海上观测目标。见图24。
7 海图上常用哪几种比例尺?
比例尺又叫做“缩尺”。是指海图上某一线段的长度与地面上相应线段水平距离之比。海图上用到的比例尺主要有三种:数字比例尺、文字比例尺和图解比例尺。
(1)数字比例尺的表现形式是怎样的?
有1:M或1/M形式,M称为比例尺分母。一般在海图中加以说明。如:1:10000或1/10000。
目前国际上通用的数字比例尺形式为1:M,如1:5000:1:25000等。
(2)文字比例尺的表现形式是怎样的?
用文字注解的方式表示。如:“图上1厘米相当于实地10千米”,“百万分之一”等。这种表示方法现在已很少用到。
(3)图解比例尺的表现形式是怎样的?
用图解形式表示的比例尺叫做图解比例尺。图解比例尺包括三种形式:直线比例尺、公里尺、复比例尺。
①直线比例尺,海图上为了量取方便和精确量测,经常在图廓东、西两侧放置直线比例尺,置于东西外图廓,长度约20~45cm。比例尺大于1:80000的民用航海图多用该直线比例尺。直线比例尺以米为单位。参见图25。

②公里尺,以公里为单位表示的直线比例尺叫公里尺,置于东西外图廓,长度基木与纵图廓线等长。军用航海图多用公里尺,因为墨卡托投影纬度具有渐长的特性,公里尺的细分也随着纬度而渐长。参见图26。

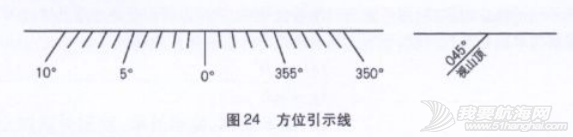
③复比例尺,或复式比例尺,因状似梯形,过去也叫梯形比例尺。在小比例尺海图上,由于变形复杂,往往在不同的经纬度有不同的变形,需要按照不同的经纬度绘制一种复式比例尺。故可认为是不同纬度比例尺的集合。可放在海图上的任何位置。包括主比例尺和局部比例尺,形状如图27。
8 什么叫主比例尺和局部比例尺?
(1)主比例尺是如何定义的?
计算地图投影时,首先将地球椭球面按一定比率缩小,然后再将其描写在平面上。这种小于1的常数比率称为地图主比例尺或普通比例尺,在地图或海图上一般都有标注,如1:50000。
(2)局部比例尺是如何定义的?

9 海图上用到哪些测量控制点?
海图上的测量控制点主要有:三角点、埋石点、水准点、独立天文点、测站点等,用来作为海图内容的平面控制点和高程控制点。
平面控制点位置用三角法测定的点称为三角点,用导线法测定的点叫做导线,点,分为一、二、三、四等级。这些都是国家级的平面控制点,如果在大比例尺测图时,平面控制点的密度不够,则各测量单位可在国家平面控制点的基础上进行加密测量,如海军布设的海道测量控制点叫做海控点,由总参谋部测绘局布设的军用控制点称为军控点。
高程控制点按测定方法和精度分为两种,一是水准点,采用几何水准测量方法测定,也分为一、二、三、四等级,二是三角高程点或高程导线点,这是在水准点密度不足时用三角高程测量方法测定的高程点,精度低于四等水准点。
海图上用三角形符号表示国家等级的三角点和导线点:用正方形符号表示埋石的或在天然岩石上凿有标志的小三角点、导线点及精度低于小三角点的控制点:用叉号和外接圆组合符号表示国家等级的水准点:用五星符号表示独立天文点,指用天文观测方法,直接测定地理坐标和方位角的点:用圆符号表示对船舶航行有方位意义的测站点或高程点。控制点符号一侧都注有数字,其中,三角点、埋石点、水准点和独立天文点符号一侧的数字表示实地上标石顶而的高程,而测站点一侧的数字表示地面高程。
10 海图用到哪些坐标系?
(1)坐标系有哪几种?
坐标系有地理坐标系和大地坐标系两种。
①地理坐标系为确定地面上点的位置,需在地球面上建立地理坐标系统,它是以地球极点为极点、由两组互相垂直的曲线所构成,一组叫做经线,一组叫做纬线。用经纬度来表示地球表面某一点的位置及地理方位,称为地理坐标系。
②大地坐标系海图上用于定位的坐标网虽然都采用地理坐标网,但由于采用大小不同的椭球和不同坐标原点的起始数据,对同一点的地理坐标值也是不同的。也就是说,由于采用不同的坐标系,使同一点的地理坐标值不同。
确定大地坐标系包括以下两方面的内容:
第一,确定椭球大小。确定大地水准面上的测量成果化算到椭球面上,计算工作中所用的椭球大小。
第二,椭球定向。确定椭球体与大地体的相关位置。其定向方法为:在适当地区选择一天文点,精密观测该点的天文经纬度、该点到大地水准面的垂直距离及该点到附近另一天文点的天文方位角。然后,将其视为该点的大地经纬度、大地方位角和大地高。确定坐标系就是确定地球椭球的形状(大小)、坐标原点和起始方位角。
(2)世界各国采用哪些坐标系?
世界各国海图采用的坐标系种类很多,因此,坐标系很不一致。其原因是各国采用的地球椭球数据(长、短半径或扁率)不相同,即采用不同的椭球参数。另外,大地坐标系的原点也不相同。
海图由许多来源不同的资料编制而成,这些资料不仅有测量资料,也有不同年代由不同国家或地区出版的陆图和海图。一个国家或同一地区的海图只有在全部经历一个改版周期之后,坐标系才能取得一致。
20世纪下半叶,空间技术发展迅速,应用航空航天和人造卫星测绘地球。缘合地面天文、大地和重力测量资料,建立了地心坐标系。如,WGS-60,WGS-66,WGS-72, WGS-84等世界坐标系。国际海道测量组织(HO)建议各国在大于1:50万航海图上都加注世界大地坐标系变换到海图坐标系的改正值说明。改正数值由美国国防部制图局提供。
如海图上加注以下类似说明:“如将本图置于WCS-84坐标系上,应将所有平行圈向南移11.5秒,所有子午圈向东移9.8秒”。
(3)我国海图用到的坐标系有哪些?
①1954年北京坐标系
新中国刚成立时,大地测量成果少,不具备建立我国独立坐标系的条件。于是就与前苏联1942年的普尔科沃大地坐标系联测,采用局部平差,于1954年在北京建立天文原点,作为全国大地控制网的起算点。
由于我国采用的克拉索夫斯基椭球体,其参数为:长半径6378245m:扁率:1:298.3。
该椭球体与我国大地水准面符合不理想,参考椭球面普遍低于大地水准面,大约平均低30米,在东南沿海地区最多低至65米。因此,用1954年北京坐标系作为我国海图的坐标系不是十分理想。
②1980年国家大地坐标系
20世纪70年代我国开始建立新的大地坐标系,于1980年初完成,定名为“1980年国家大地坐标系”。椭球参数采用国际大地测量与地球物理联合会1975年推荐的数值:长半径6378140m:扁率:1:298.245.大地坐标系原点位于陕西省泾阳县水乐店。
③整体平差值的1954年北京坐标系
尽管1954年北京坐标系不太精确,但为了避免1980年国家大地坐标系给地图测绘带来较大影响,考虑到我国测绘的现状,我国在1980年坐标系基础上,又建立了“整体平差值的1954年北京坐标系”,也叫新1954年北京坐标系。椭球参数仍然采用克拉索夫斯基椭球体。由此可见,新1954年北京坐标系是由1980年新国家大地坐标系派生得来的,是作为老54系到80系的过渡而存在的。
新、老54北京坐标系不存在椭球差异和定位差异,两系统同一点坐标的不同主要是由于一个是全国统一平差的结果,而另一个则是局部平差结果的缘故所产生的。
④WGS-84世界坐标系
WGS-84坐标系(Vord Geodetic System1984)是美国国防部研制确定的大地坐标系,是一种协议地球坐标系。WGS-84坐标系的原点是地球的质心,空间直角坐标系的Z轴指向地极方向,X轴指向零子午面和赤道的交点,Y轴和乙、X轴构成右手坐标系。
WGS-84椭球采用国际大地测量与地球物理联合会第17届大会测量常数推荐值,采用的两个常用参数为:长半径6378137m,扁率1:298.257223563由于国际海道测量组织建议各国海图采用WGS-84坐标系,因此,我国海图生产部门,近几年来对海图坐标系进行了改算。
⑤2000年大地坐标系
2000年大地坐标系又称中国大地坐标系2000(China Geodetic Coordinate System2000, CGCS2000)简称“2000国家大地坐标系”,为地心三维坐标系统。2000年大地坐标系的原点是地球的地心(也称质心),两个常用参数为:长半径6378137m,扁率1:298.257222101,该参数与WCS-84坐标系的参数值非常接近。2008年7月1日正式启用,今后我国海图都采用该坐标系,凡海图资料采用其他坐标系的,一般将予以改算。
(4)海图平面坐标系有哪些?
海图要素是建立在平面上的,因此,在海图上建立的坐标有平面直角坐标系和平面极坐标系两种。它是通过投影方法把地球表面上的经纬线网、控制点的地理坐标转换成平面直角坐标。平面直角坐标便于计算和展绘。
墨卡托投影海图上一般表示经纬线格网和控制点:
高斯一克吕格投影海图上一般表示经纬线格网,而地形图上则表示平面直角坐标网,称为方里网或公里网。为转绘资料方便,常在墨卡托投影海图上加绘高斯公里网。要求加网范围略大于制图区域。
11 海图的高程基准与深度基准是如何确定的?
海图的高程基准面和深度基准面,总称为海图基准面(Chart datum,CD)。
(1)高程基准面是如何确定的?
海图上高程的起算面,叫做海图的高程基准面。海图上的山峰、岛屿、明礁的高程都从高程基准面向上算起。高程基准面是根据验潮站所确定的多年平均海水面确定的。海图上的高程是地面点至平均海面的垂直高度。1956年以前,我国没有统一的高程基准面,而是采用了当地的平均海面,如大连平均海面、大沾平均海面、黄河口零点(平均海面)、青岛平均海而、坎门平均海面、吴淞平均海面、珠江基而等。1957年确定,根据青岛验潮站1950~1956年共7年间的验潮资料求得的平均海面作为国家统一的高程基准面,并定名为“1956年黄海平均海面”,该平均海面在青岛观象山上的水准点下72.289米。
由于1956年黄海平均海面只用了7年的险潮资料计算得到的,并且在最初两年的验潮资料还有错误。所以该平均海面不太精确。20世纪70年代,我国提出了新的高程基准面方案。采用青岛验潮站1952~1979年27年中19年的潮汐观测资料重新计算确定,定名为“1985年国家高程基准”。1987年报请国务院批准,1988年1月1日正式启用。1985年国家高程基准在青岛观象山水准原点下72.260米,与1956年黄海平均海面相差-0.029米。
世界各国海图所采用的高程基准面都不一致。英、美等国过去曾采用平均大潮高程面作为海图的高程起算面。但现在大多数国家都以平均海面作为高程起算面。其确立方法都是以某一地点验潮站多年观测资料计算的多年平均海面为基准设立统一的大地原点,以建立统一的高程系统。
(2)深度基准面是如何确定的?
深度基准面是海图上水深的起算面。从深度基准面至水底之间的垂直距离称为“图载水深”。水深测量是在随时升降的水面上进行的,因此,在同一点上不同时刻测得的水深值不同。为此,必须确定一个起算面,把不同时刻测得的某点水深归算到这个面上,这个面就是深度基准面。深度基准面通常在当地平均海面下某一深度值处。求算深度基准面的原则是既考虑到舰船航行的安全,又要考虑到航道的利用率。一般保证率在90,-95%之间。
世界各国所采用的深度基准面也不相同,一般采用理论最低潮面,平均低潮面、最低低潮面、平均大潮低低潮面、略最低潮面、平均海面、平均大潮低潮面、赤道大潮低潮面等。世界部分国家、地区采用的深度基准面情况如表11一1:

我国1956年以前的海图上一般采用略最低潮面(印度大潮低潮面),从1956年开始采用理论深度基准面,1991年起改称为理论最低潮面。理论最低潮面是理论上可能出现的最低潮面,位于平均海面以下高度为L的平面处,随着海区潮差大小不同,L值也不同。为什么要采用理论最低潮面来作为深度基准面?主要是根据确定深度基准面的原则,经过长期的实践证明,只有理论最低潮面才最符合我国海区的潮汐情况,才能提高航行保证率。
(3)海图上高程基准面与深度基准面的关系是怎样确定的?
海图上的各种上下起伏要素都是从高程基准面和深度基准面向上或向下起算,这些起算面主要包括山高、岛高、明礁高、干出高、水深、暗礁深度等起算面。各种起伏要素的起算面及其起算方向规定如下:
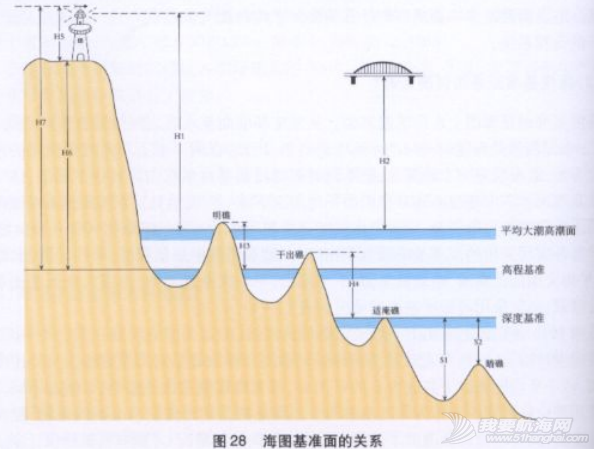
海图上的灯高,规定从大潮高潮面向上起算至灯光中心的距离:
山、岛等正向地貌的高程都从高程基准面向上起算:
礁石采用不同的基准面:明礁的高程与山、岛高程一样,都是从高程基准面向上起算:暗礁侧从深度基淮面向下起算;干出礁、干出避上的干出高度则从深度基准面向上起算:适淹礁侧是位于深度基准面上的礁石。图28中,H1表示灯高;H2为净空高度:H3为明礁高度:
H4为干出高度:H5为建筑物比高;H6为高程;H7为建筑物顶高:S1为水深:S2为暗礁深度。
由此可见,海图上的基准面不但决定了海图上的安全水深,还决定了礁石的性质。由于海图上的几个起算面相差较大,对理解海图上某些起伏要素的性质有一定帮助,因此,有必要了解海图上几个基准面的图解关系。
12 海图上常用的单位有哪些?
海图上常用的单位主要有距离单位、深度或高度单位、时间单位、速度单位、重量单位和角度单位。
(1)距离单位有哪些?
海图上常用的距离单位有千米、米、海里、链等。
千米是最常用的距离量测单位,习惯上也叫公里,其英文为kilometre,缩写为km:
米是目前国际上通用的基准长度单位。其大小为通过巴黎子午圈长的四千万分之一。其英文为metre,缩写为m。
海里也是计量海上距离的常用单位,其英文为nautical mile,缩写为M或n mile。.海图上1海里为地球面经线上纬度1'的长度。1海里在不同纬度处的长度不同。由于每个国家所处的纬度不同,规定1海里的长度也就不相等,为此,1929年有关国际会议通过地球纬度1分的平均长度为1852米,我国也采用1852米作为1海里的长度,即:1海里=1.852千米=1852米。
十分之一海里称为1链,约200码。即:1链=0.1海里。链的英文单词为cble。
(2)深度或高度单位有哪些?
海图上常用的深度或高度单位主要有米、分米、厘米、毫米、英尺、英寻等。这些单位的英文名称及其缩写分别为:米(metre,m)、分米(decimeter,dm)、厘米(centimeter,cm)、毫米(millimeter,mm)、英尺(feet,t)、英寻(fathom)c现在海图上的水深以米为单位,过去的海图曾用过英寻或英尺,它们之间的换算关系为:1英寻=6英尺=1,8米。
(3)时间单位有哪些?
海图上用到的时间单位主要有小时(hour,h)、分(minute,min)、秒(second,sec)。主要用于灯质注记等,如“闪3秒”。
(4)速度单位有哪些?
海图上表示的潮流流速、海流流速或风速等都用节表示,它是国际航海上通用的速度单位。节的英文名称为knot,简写为kn,相当于海里/小时。即:1节=1海里/小时。
(5)重量单位有哪些?
重量单位用吨表示,其英文为to,缩写为t.1吨等于1000千克。多用于表示码头附近的固定式起重机和集装箱的起吊重量单位。
(6)角度单位有哪些?
角度单位用度(degree)、分(minute ofarc),秒(secondofare)表示。I度等于直角的1/90,用空心的小圆符号“”表示。度分秒之间的换算关系都是60,即:1°=60'(分),1'=60“(秒)。多用于表示地理经纬度和方位。
|